$\{(8(5-x)>3(x-5)),(3x^2-10x+3>0):}$

A cura di: Francesco Speciale

${(8(5-x)>3(x-5)),(3x^2-10x+3>0):}$

---

${(8(5-x)>3(x-5)),(3x^2-10x+3>0):}$;
${(40-8x>3x-15),(3x^2-10x+3>0):}$;
Semplificando
${(-11x> -55),(3x^2-10x+3>0):}$;
Cambiando di segno
${(x<5),(3x^2-10x+3>0):}$;
Studiamo la disequazione di secondo grado

$3x^2-10x+3>0$

$(Delta)/4=(b/2)^2-ac=(-5)^2-(3*3)=25-9=16$
$x_(1,2)=(-b/2+-sqrt((Delta)/4))/a=(5+-sqrt(16))/3=(5+-4)/3 => x_1=3 ^^ x_2=1/3$.

Siccome il segno del coefficiente di $x^2$ è concorde col segno della disequazione,
prenderemo gli intervalli esterni, quindi soluzione della disequazione sarà:
$x<1/3 vv x>3$.
Pertanto
${(x<5),(x<1/3 vv x>3):}$;
Soluzione del sistema sarà l’intersezione delle singole soluzioni delle disequazioni che lo compongono.

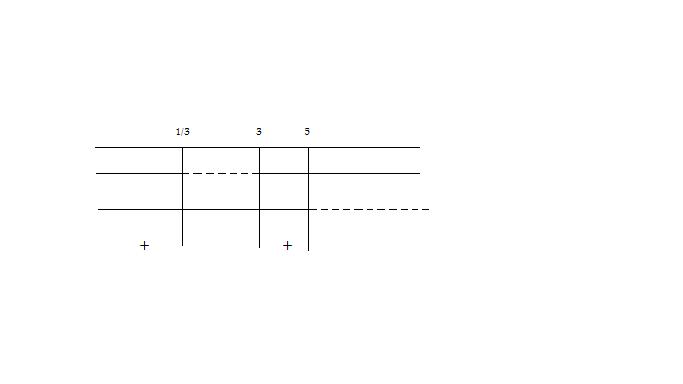
Quindi la soluzione sarà:$x<1/3 vv 3<x<5$.