I numeri complessi

I NUMERI COMPLESSI. I numeri complessi sono largamente usati, non solo ovviamente in matematica ma anche in fisica ed in molti campi dell’ingegneria, vista le loro proprietà nel descrivere fenomeni di natura ondulatoria.
I numeri complessi formano un campo indicato generalmente con la ? e si possono rappresentare (vedi figura successiva) sul piano complesso o anche detto di Gauss. Da notare comunque che ha Gauss va dato il merito di alcune pubblicazioni che hanno portato all’uso nell’ambiente matematico di tale famiglia di numeri, ma in realtà i primi passi nell’analisi complessa furono fatti già da Eulero e De Moivre.

Un numero complesso si può individuare sul piano con una coppia di coordinate (a,b), dove a viene chiamata parte reale e b invece parte immaginaria. In generale possiamo riscrivere questo numero come:

z=a+ib

Con la lettera i (talvolta nei testi potrete trovare la lettera j, non vi spaventate è la stessa cosa) indichiamo quello che viene chiamato coefficiente dell’immaginario, che per definizione sarà pari:

i?√(-1)

I numeri con parte reale nulla sono detti inoltre immaginari puri, esempio: z=i2.
Un’altra espressione dei numeri complessi la si può fare sfruttando il fatto che essendo individuati da una coppia di punti su un piano, un numero è rappresentato come un vettore quindi se ne può trovare modulo e angolo. Tale rappresentazione viene detta in coordinate polari ed è più sfruttata in ambito universitario e nei settori scientifici in generale.

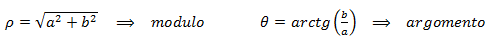
Prima di passare alle operazioni con i numeri complessi vediamo che è possibile definire elemento neutro e opposto del numero complesso esattamente come nel campo reale. In più possiamo definire il complesso coniugato di un numero.

Elemento neutro:
Rispetto la somma abbiamo l’origine degli assi (0,0);
Rispetto il prodotto abbiamo il punto individuato da (1,0), questo è possibile dimostrarlo una volta definita l’operazione di prodotto, che vedremo sarà un po’ particolare.

Opposto:
definito il numero complesso come z=a+ib il suo opposto sarà z ?=-a-ib.

Complesso coniugato:
se z=a+ib allora il complesso coniugato sarà  z ?=a-ib. Ovvero graficamente è il simmetrico rispetto l’asse delle ascisse.

Ora definiamo le operazione base matematiche:

Somma:
presi due numeri complessi z=a+ib  e  w=c+id

z+w=(a+c)+i(b+d)

Quindi si sommano parte reale con parte reale e parte immaginaria con parte immaginaria. Un discordo simile si fa con la sottrazione.

Sottrazione:

z-w=(a-c)+i(b-d)

Prodotto:
discorso a parte per il prodotto, di fatti non va bene né quello scalare né tantomeno quello vettoriale, si verifica tramite gli assiomi di campo che il prodotto tra due numeri complessi si può scrivere come:

z×w=(ac-bd)+i(ad+bc)

Quoziente:
per il quoziente si sfrutta il complesso coniugato. Si moltiplica e si divide per il complesso coniugato, vediamo come:

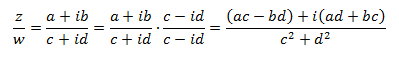
Facciamo un esempio. Presi i numeri z=2-i e w=3+i, se ne faccia somma, differenza, prodotto e quoziente.

z+w=(2+3)+i(-1+1)=5

z-w=(2-3)+i(-1-1)=-1-i2

Per il prodotto possiamo sfruttare o la regola scritta prima, o possiamo fare il prodotto algebrico, vedremo sarà la stessa cosa.

z×w=[2?3-(-1)?1]+i[2?1+(-1)?3]=7-i

z×w=(2-i)(3+i)=6+2i-3i-i^2=6+2i-3i+1=7-i

Vediamone ora una semplice applicazione in cui troviamo i numeri complessi. Risoluzione dell’equazione:

x²+2x+2=0

Se si calcola il discriminante vedremo che sarà minore di zero, quindi avremo sotto radice una quantità minore di zero, ed è proprio qui che entrano in gioco i numeri complessi.

Un’equazione di secondo grado che ha come soluzioni due radici complesse e coniugate.