Matrici

Una matrice è un'entità matematica costituita da un insieme di numeri, disposti ordinatamente secondo righe e colonne. In particolare una matrice m × n è un insieme di mn numeri racchiusi tra due parentesi, disposti a formare m righe e n colonne. Ad esempio:

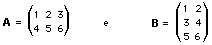
sono matrici 2 × 3 e 3 × 2. Gli elementi di una matrice possono essere numeri interi, razionali, reali o complessi. L'elemento dell'i-esima riga e della j-esima colonna di una matrice A si indica con a_ij o (A)_ij.

Si può dire che una matrice m × n raccoglie mn informazioni a_ij, indicizzate dai due parametri i, j. Ad esempio, dati m paesi che esportano n prodotti ciascuno, a_ij potrebbe rappresentare la quantità del j-esimo prodotto esportato dall'i-esimo paese in un dato anno, cosicché ogni riga o ogni colonna di A rappresenterebbe rispettivamente un paese o un prodotto.

L'esigenza di elaborare informazioni di questo tipo porta a una teoria algebrica in cui le operazioni base dell'aritmetica vengono applicate a intere matrici. Se A e B sono entrambe matrici m × n (matrici che posseggono un diverso numero di righe e colonne non possono essere né sommate, né sottratte), la somma A + B si ottiene sommando ordinatamente gli elementi corrispondenti, ovvero (A + B)_ij = a_ij + b_ij. Ad esempio:

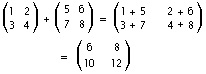
La differenza A – B è definita in modo analogo dalla relazione (A – B)_ij = a_ij – b_ij. Così, se A e B rappresentano le esportazioni relative a due anni consecutivi, la matrice A + B indica l'ammontare complessivo delle esportazioni del periodo dei due anni; se C rappresenta il totale delle importazioni del primo anno, allora A – C fornisce le esportazioni nette di quell'anno.

Se A è una matrice m × n, e B è una n × s, il prodotto AB è una matrice m × s il cui elemento generico (AB)_ij è dato dall'i-esima riga della matrice A e dalla j-esima colonna di B secondo la formula (AB)_ij = a_i1b_1j + a_i2b_2j +…+ a_inb_nj. Ad esempio:

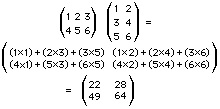
Tornando all'esempio delle esportazioni, se D è una matrice n × 1 (vettore colonna) i cui elementi sono i costi per quantità unitarie degli n prodotti, allora AD è una matrice m × 1 i cui elementi rappresentano i valori delle esportazioni degli m paesi.

Una matrice quadrata è una matrice n × n, per qualunque n dato, ossia una matrice che contiene numero uguale di righe e di colonne. Date due matrici A e B entrambe n × n, allora le matrici A + B, A – B, AB e BA sono anch'esse matrici n × n. L'algebra delle matrici quadrate assomiglia per molti aspetti all'algebra dei numeri (con le debite eccezioni: ad esempio non vale la proprietà commutativa del prodotto, cosicché AB può essere diversa da BA). La matrice identità I definita da:

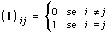
soddisfa la relazione IA = AI = A per tutte le matrici A, così come il numero 1 in campo numerico.
A ogni matrice n × n, che supponiamo di indicare con A, si può associare un numero detto determinante e indicato generalmente con det (A). Se n = 1, det(A) = a11; se n > 1 allora:

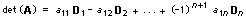
dove D_j (detto minore di A) è il determinante della matrice (n – 1) × (n – 1) ottenuta rimovendo la prima riga e la j-esima colonna di A. Si può dimostrare che se det (A) ≠ 0, allora A ammette la matrice inversa A^(-1), che soddisfa la relazione AA^(-1) = A^(-1)A = I.

La matrice trasposta A^t di una matrice A si ottiene scambiando le righe con le colonne, ossia, per ogni i e j, vale (At)_ij = a_ji. Una matrice quadrata si dice ortogonale se A^tA = I.
L'aggiunta di una matrice A, che si indica con A*, si ottiene cambiando tutti i numeri complessi che compaiono fra gli elementi di At con il rispettivo complesso coniugato (che equivale a cambiare il segno della parte immaginaria). Una matrice si dice unitaria se A*A = I. Le matrici unitarie sono particolarmente importanti in fisica, in modo particolare in meccanica quantistica, dove rappresentano speciali trasformazioni dello spazio, che conservano determinati parametri dei sistemi fisici.

Le matrici sono estremamente utili per la soluzione dei sistemi di equazioni lineari e sono largamente utilizzate in geometria. La posizione di un punto in un sistema di riferimento tridimensionale è individuata da una terna di numeri, le coordinate x, y e z. A ogni punto si può quindi associare un semplice vettore colonna, e a un insieme di punti si fa corrispondere un insieme di vettori colonna. In questo modo le trasformazioni geometriche, come ad esempio una rotazione intorno a un punto o la riflessione nel piano, possono essere rappresentate in termini di moltiplicazioni e somme fra matrici opportune. Lo stesso vale per i problemi astratti che riguardano spazi n-dimensionali, utilizzando matrici di dimensione superiore a tre.