Un numero naturale si dice primo se è divisibile solo per $1$ e per se stesso
Ad esempio, i numeri $5, 11, 23$ rispettivamente divisibili per $1$ e $5$, per $1$ e $11$ e per $1$ e $23$, sono primi.
Il procedimento per stabilire se un numero è primo è quello di verificare se è divisibile per tutti i numeri che lo precedono. Per velocizzare questa operazione adottiamo un metodo noto con il nome di crivello di Eratostene. Applichiamo tale tecnica alla ricerca dei numeri primi compresi fra $1$ e $60$.
Iniziamo costruendo un elenco (detto setaccio) con i numeri compresi fra i due estremi della ricerca:
| $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| $11$ | $12$ | $13$ | $14$ | $15$ | $16$ | $17$ | $18$ | $19$ | $20$ |
| $21$ | $22$ | $23$ | $24$ | $25$ | $26$ | $27$ | $28$ | $29$ | $30$ |
| $31$ | $32$ | $33$ | $34$ | $35$ | $36$ | $37$ | $38$ | $39$ | $40$ |
| $41$ | $42$ | $43$ | $44$ | $45$ | $46$ | $47$ | $48$ | $49$ | $50$ |
| $51$ | $52$ | $53$ | $54$ | $55$ | $56$ | $57$ | $58$ | $59$ | $60$ |
Eliminiamo dalla tabella il numero $1$ che per convenzione si è deciso di non inserire fra i numeri primi. Il primo numero primo è il $2$; lo segniamo in rosso ed eliminiamo (setacciamo) tutti i suoi multipli.
| $2$ | $3$ | $5$ | $7$ | $9$ | |||||
| $11$ | $13$ | $15$ | $17$ | $19$ | |||||
| $21$ | $23$ | $25$ | $27$ | $29$ | |||||
| $31$ | $33$ | $35$ | $37$ | $39$ | |||||
| $41$ | $43$ | $45$ | $47$ | $49$ | |||||
| $51$ | $53$ | $55$ | $57$ | $59$ |
Il secondo numero è il $3$; analogamente al passaggio precedente, segniamolo in rosso ed eliminiamo tutti i suoi multipli. Otteniamo:
| $2$ | $3$ | $5$ | $7$ | ||||||
| $11$ | $13$ | $17$ | $19$ | ||||||
| $23$ | $25$ | $29$ | |||||||
| $31$ | $35$ | $37$ | |||||||
| $41$ | $43$ | $47$ | $49$ | ||||||
| $53$ | $55$ | $59$ |
Ripetiamo lo stesso procedimento colorando il $5$ ed eliminando i suoi multipli.
| $2$ | $3$ | $5$ | $7$ | ||||||
| $11$ | $13$ | $17$ | $19$ | ||||||
| $23$ | $29$ | ||||||||
| $31$ | $37$ | ||||||||
| $41$ | $43$ | $47$ | $49$ | ||||||
| $53$ | $59$ |
Applichiamo nuovamente la procedura con il $7$
| $2$ | $3$ | $5$ | $7$ | ||||||
| $11$ | $13$ | $17$ | $19$ | ||||||
| $23$ | $29$ | ||||||||
| $31$ | $37$ | ||||||||
| $41$ | $43$ | $47$ | |||||||
| $53$ | $59$ |
Ripetendo tale procedimento otteniamo una tabella con molte caselle vuote; i numeri rimasti sono tutti ed i soli numeri primi compresi fra $1$ e $60$.
Scomposizione in fattori primi
Consideriamo dei numeri non primi, ovvero dei numeri che si compongono di più fattori moltiplicati tra loro:
$$14=7cdot 2quadquad 18=9cdot 2quadquad 20=5cdot 4$$
Nei tre casi abbiamo operato una scomposizione del numero in fattori. Spesso è necessario ottenere una scomposizione in cui i fattori siano tutti numeri primi.
Per comprendere il procedimento da utilizzare consideriamo, ad esempio, il numero $108$.
Una sua scomposizione in fattori è data dal prodotto $12cdot 9$.
Ciascuno di tali fattori è a sua volta scomponibile in altri fattori:
- $12$ può essere scomposto nella forma $4cdot 3$ (che a sua volta si può scrivere nella forma $2^2cdot 3$);
- $9$ può essere scomposto nella forma $3^2$.
In definitiva possiamo scrivere:
$$108=12cdot 9=(4cdot 3)cdot(3^2)=2^2cdot 3cdot 3^2=2^2cdot 3^3$$
L'operazione che ci permette di scrivere un numero composto come prodotto di fattori primi si dice scomposizione in fattori primi o fattorizzazione.
Un metodo pratico per svolgere la scomposizione in fattori primi di un numero, ad esempio $132$, è il seguente:
- tracciamo alla destra della destra del numero una linea verticale;
- applichiamo i criteri di divisibilità e scriviamo a destra del numero il più piccolo divisore del numero (cioe $2$);
- calcoliamo la divisione fra il numero ed il divisore ($132:2$) e scriviamo il risultato ($66$) immediatamente sotto il numero $132$;
- scriviamo a destra di $66$ il divisore più piccolo (ancora il numero $2$) e sotto al $66$ il risultato della divisione ($33$);
- scriviamo a destra di $33$ il divisore più piccolo (il numero $3$) e sotto il $33$ il risultato della divisione ($11$);
- il numero $11$ è primo quindi lo riscriviamo alla sua destra e, al solito, riportiamo sotto il suo quoziente ($1$).
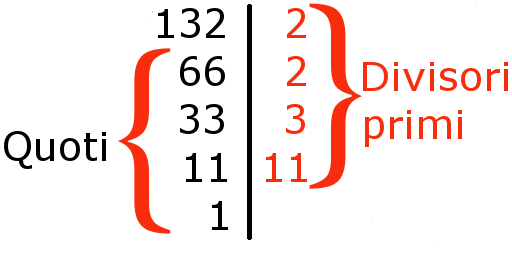
Avendo trovato come quoziente il numero $1$, la procedura di scomposizione è terminata e possiamo scrivere:
$$132=2cdot 2cdot 3cdot 11=2^2cdot 3cdot 11$$
Esempio
Scomporre in fattori primi il numero $126$
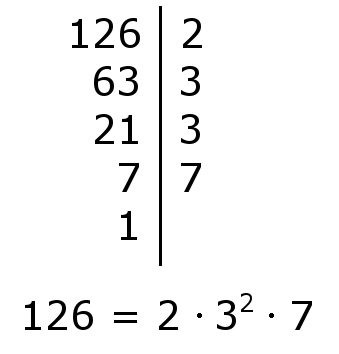
Esempio
Scomporre in fattori primi i numeri $3780$ e $252$

Scomponi ciascuno dei seguenti numeri in prodotti di fattori primi.
$$38;quadquad 200;quadquad 622;quadquad 1656;quadquad 16016.$$
MCD e mcm
Dati due numeri naturali, ad esempio il $12$ e il $16$, calcoliamo i loro insiemi dei divisori:
$$D_{12}={1, 2, 3, 4, 6, 12}quadquad D_{16}={1, 2, 4, 8, 16}$$
Osserviamo che l'insieme dei divisori comuni ad entrambi i numeri è costituita dai numeri $1, 2$ e $4$ cioè $D_{12, 16}={1, 2, 4}.
Il numero $4$ è il maggiore di tali divisori comuni e per tale ragione viene chiamato Massimo Comune Divisore (M.C.D.) dei numeri $12$ e $16$; in simboli:
$$M.C.D.(12, 16)=4$$
Il M.C.D. di due o più numeri è il maggiore tra i divisori comuni ai numeri dati.
Inoltre:
Due o più numeri si dicono primi tra loro se hanno $1$ come M.C.D.
Esempio
Calcoliamo il M.C.D. tra i numeri $18, 24, 30$.
Scriviamo tutti i loro divisori:
$$begin{array}{l} D_{18}={1, 2, 3, 6, 9, 18}\ D_{24}={1, 2, 3, 4, 6, 8, 12, 24}\ D_{30}={1, 2, 3, 5, 6, 10, 15, 30}end{array}$$
I divisori comuni di $18, 24$ e $30$ costituiscono l'insieme $D_{18, 24, 30}={1, 2, 3, 6}$; il maggiore di essi è il numero $6$ e pertanto:
$$M.C.D.(18, 24, 30)=6$$
Calcola il M.C.D. di ciascuno dei seguenti gruppi di numeri mediante la fattorizzazione.
- 1) $(60, 72)$
- 2) $(110, 28)$
- 3) $(900, 810)$
- 4) $(92, 161, 506)$
- 5) $(675, 450, 1000)$
Consideriamo adesso due numeri naturali, ad esempio il $2$ e il $3$ ed elenchiamo in ordine crescente alcuni loro multipli (escluso lo zero):
$M_2={2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24,dots}$
$M_3={3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33,dots}$
Osserviamo che l'insieme dei multipli a comune tra i due numeri è l'insieme:
$$M_{2, 3}={6, 12, 18, 24,dots}$$
Il numero $6$ è il minore di tanti multipli comuni e per questa ragione viene detto minimo comune multiplo (m.c.m) dei numeri $2$ e $3$; in simboli:
$$m.c.m.(2, 3)=6$$
Il m.c.m. di due numeri è il minore tra i multipli comuni ai numeri stessi.
Esempio
Calcoliamo il m.c.m. dei numeri $3, 4, 6$.
Scriviamo alcuni loro multipli:
$$begin{array}{l} M_{3}={3, 6, 9, 12, 15, 18, 21, 24, 27,dots}\ M_{4}={4, 8, 12, 16, 20, 24, 28,dots}\ M_{6}={6, 12, 18, 24, 30, 36,dots}end{array}$$
I multipli comuni di $3, 4$ e $6$ costituiscono l'insieme $M_{3, 4, 6}={12, 24,dots}$; il minore di essi è il numero $12$ e pertanto:
$$m.c.m.(3, 4, 6)=12$$
Calcola il m.c.m. di ciascuno dei seguenti gruppi di numeri mediante la fattorizzazione.
- 1) $(75, 60)$
- 2) $(420, 225)$
- 3) $(900, 810)$
- 4) $(210, 525, 735)$
- 5) $(1200, 800, 360)$


