A cura di: Francesco Speciale
Risolvi in $RR$ la seguente disequazione frazionaria
$(x^2-2x)/(x^2+5x+13)<0$
$(x^2-2x)/(x^2+5x+13)<0$;
Il denominatore e il numeratore devono, quindi, avere segni discordi.
Il denominatore risulta essere positivo $AA x in RR$.
Studiamo ora il numeratore, ponendolo minore di zero
$x^2-2x<0$;
$x(x-2)<0 => 0<x<2$
(Siccome il coefficiente di $x^2$ e il segno della disequazione sono discordi,
prenderemo come soluzione accettabile l’intervallo interno)
Ora intersechiamo le soluzioni riguardanti il numeratore e il denominatore, ricavando così la soluzione della disequazione
L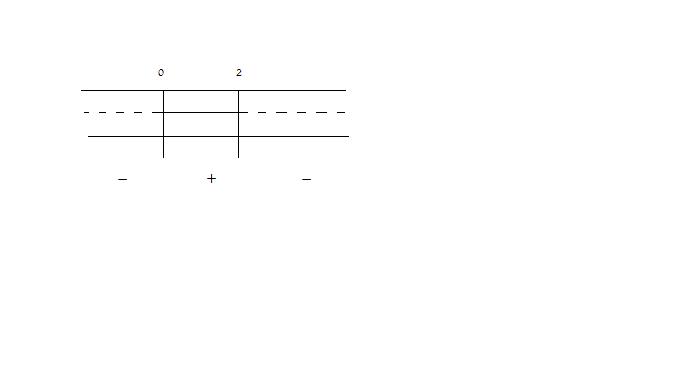
a soluzione sarà $0<x<2$.
- Disequazioni