A cura di: Francesco Speciale
Si determini l’equazione della circonferenza con centro nell’origine e raggio $1$.
Svolgimento
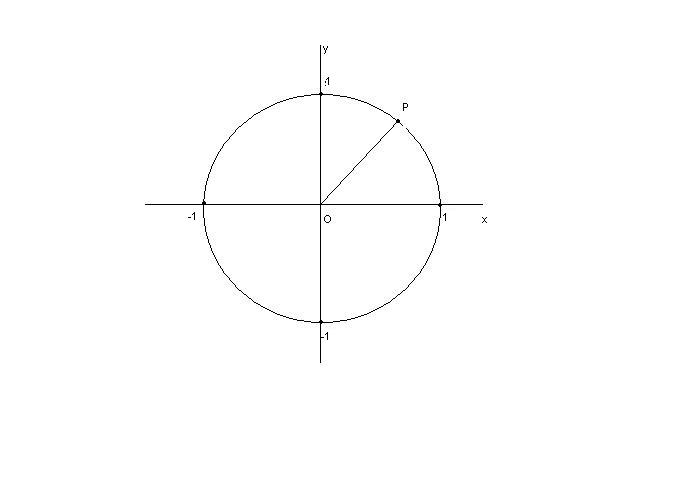I punti appartenenti a questa circonferenza sono quelli aventi distanza dall’origine pari a $1$,
cioè la circonferenza considerata è il luogo geometrico dei punti $P$ del piano per cui si ha:
$bar{OP}=5$.
Indicando con $(x,y)$ le coordinate del generico punto $P$ e tenendo presente la formula che esprime
la distanza tra due punti nel piano cartesiano:
$d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)$
L’eguaglianza $bar{OP}=1$, la possiamo così riscrivere:
$sqrt((x-0)^2+(y-0)^2)=1$;
$sqrt(x^2+y^2)=1$
Elevando al quadrato ambo i membri dell’equazione
$x^2+y^2=1$;
$x^2+y^2-1=0$
Quest’ultima rappresenta l’equazione della circonferenza con centro nell’origine e raggio $1$.
- Geometria
