$sqrt(x^2-2x-1)

A cura di: Francesco Speciale

$sqrt(x^2-2x-1)<x-1$

---

$sqrt(x^2-2x-1)<x-1$;
L’indice della radice è pari ed è del tipo $sqrt(f(x))>g(x)$ quindi sarà equivalente al sistema:

${(f(x)>=0),(g(x)>0),(f(x)<[g(x)]^2):}$;
Nel nostro caso $f(x)=x^2-2x-1 ^^ g(x)=x-1$.
Quindi la disequazione è equivalente al sistema:
${(x^2-2x-1>=0),(x^2-2x-1<(x-1)^2),(x-1>0):}$;
${(x^2-2x-1>=0),(x^2-2x-1<x^2-2x+1),(x>1):}$
${(x^2-2x-1>=0),(-1<+1),(x>1):}$
La seconda disequazione è verificata$AA x in RR$.

Studiamo singolarmente la disequazione di secondo grado:
$x^2-2x-1>=0$

$(Delta)/4=(b/2)^2-ac=(-1)^2-(1*(-1))=1+1=2$
$x_(1,2)=(-b/2+-sqrt((Delta)/4))/a=(1+-sqrt2) => x_1=(1-sqrt2) ^^ x_2=(1+sqrt2)$.

Siccome il segno del coefficiente di $x^2$ è concorde col segno della disequazione,
prenderemo gli intervalli esterni, quindi soluzione della disequazione sarà:
$S_2={x<=(1-sqrt2) vv x>=(1+sqrt2)}$.

Intersechiamo, ora, le soluzioni trovate e otterremo la soluzione finale del sistema

 

 

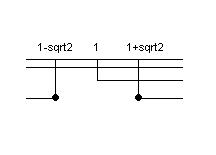
$S={x>=(1+sqrt2)}$.