A cura di: Francesco Speciale
$sqrt(x^2-3)-sqrt(4x-5)<=0$
$sqrt(x^2-3)-sqrt(4x-5)<=0$;
Riscriviamo l’equazione nel seguente modo
$sqrt(x^2-3)<=sqrt(4x-5)$;
Per l’esistenza della disequazione deve essere:
${(x^2-3>=0),(4x-5>=0):}$;
${(x^2>=3),(x>=5/4):}$;
${(x<=-sqrt3 vv x>=sqrt3),(x>=5/4):}$;
L’unione delle soluzioni sarà:

$S={x>=sqrt3}$
In tale condizione i due membri sono positivi, elevando al quadrato si deve risolvere il sistema:
${((sqrt(x^2-3))^2<=(sqrt(4x-5))^2),(x>=sqrt3):}$;
${(x^2-3<=4x-5),(x>=sqrt3):}$;
${(x^2-4x+2<=0),(x>=sqrt3):}$;
Studiamo la disequazione di secondo grado:
$x^2-4x+2<=0$
$(Delta)/4=(b/2)^2-ac=(-2)^2-(1*2)=4-2=2$
$x_(1,2)=(-b/2+-sqrt((Delta)/4))/a=(2+-sqrt2)=> x_1=(2+sqrt2) ^^ x_2=(2-sqrt2)$.
Siccome il segno del coefficiente di $x^2$ è discorde col segno della disequazione,
prenderemo gli intervalli interni, quindi soluzione della disequazione sarà:
$(2+sqrt2)<=x<=(2+sqrt2)$.
L’intersezione delle soluzioni, darà la soluzione finale
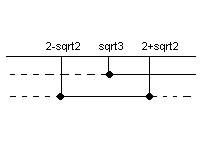
$S={sqrt3<=x<=2+sqrt}$.