Seconda Prova Matematica Maturità 2024 al Liceo Scientifico
La Maturità 2024 è in pieno svolgimento, ma oggi finiscono gli scritti. Questa mattina gli studenti del Liceo Scientifico sono stati alle prese con i quesiti di Matematica. Per i maturandi del Liceo scientifico, la seconda prova consiste in:
- la risoluzione di 1 problema a scelta tra i 2 proposti;
- la risoluzione di 4 quesiti a scelta tra gli 8 proposti.
I quesiti spaziano tra algebra, geometria e aritmetica, dando modo agli studenti di scegliere i problemi e le domande in cui si sentono più preparati, massimizzando così le opportunità di ottenere un buon punteggio.
Seconda Prova Matematica Maturità 2024: le tracce
Ecco il testo della Seconda prova di Maturità 2024 per il Liceo Scientifico:

Seconda Prova Matematica Maturità 2024: soluzioni
Come Seconda Prova di Matematica alla Maturità 2024 troviamo due problemi e 8 quesiti, con una serie di prove di geometria, equazioni e funzioni. Entrambi i problemi di Matematica sono due classici studi di funzione. Il primo ha un’impostazione classica e non presenta alcun riferimento alla realtà. Il secondo, invece, ha sì un’impostazione classica, tuttavia riporta due frasi che vogliono aiutare a contestualizzare il problema, pur non entrando poi nello svolgimento pratico.
Gli 8 quesiti di matematica riguardano analisi matematica, calcolo delle probabilità, geometria piana e analitica. Non mancano invece in queste domande riferimenti alla realtà: dal triangolo isoscele alla moneta truccata, passando per una citazione di Gadda e per la descrizione matematica dell’orbita della Terra intorno al sole. La prima frase contenuta in una delle tracce è del matematico italiano Ennio De Giorgi: “All’inizio e alla fine, abbiamo il mistero…A questo mistero la matematica ci avvicina, pur senza penetrarlo“. La seconda frase è, invece, del matematico britannico Hardy: “Le forme create dal matematico, come quelle create dal pittore o dal poeta, devono essere belle: le idee, come i colori o le parole, devono legarsi armoniosamente. La bellezza è il requisito fondamentale: al mondo non c’è posto perenne per la matematica brutta“.
Problema 1
Il primo problema tratta lo studio di una funzione con due parametri ed è un problema standard. Nel primo punto i maturandi sono chiamati a trovare l’equazione di una retta tangente al grafico della funzione. Poi devono svolgere lo studio di funzione, una volta fissati i parametri, e ancora lavorare sulle rette tangenti e le loro intersezioni con il grafico della funzione. Attraverso un integrale definito devono poi trovare l’area compresa tra il grafico della funzione e alcune rette caratteristiche (un asintoto obliquo e una delle tangenti trovate precedentemente).
Problema 2
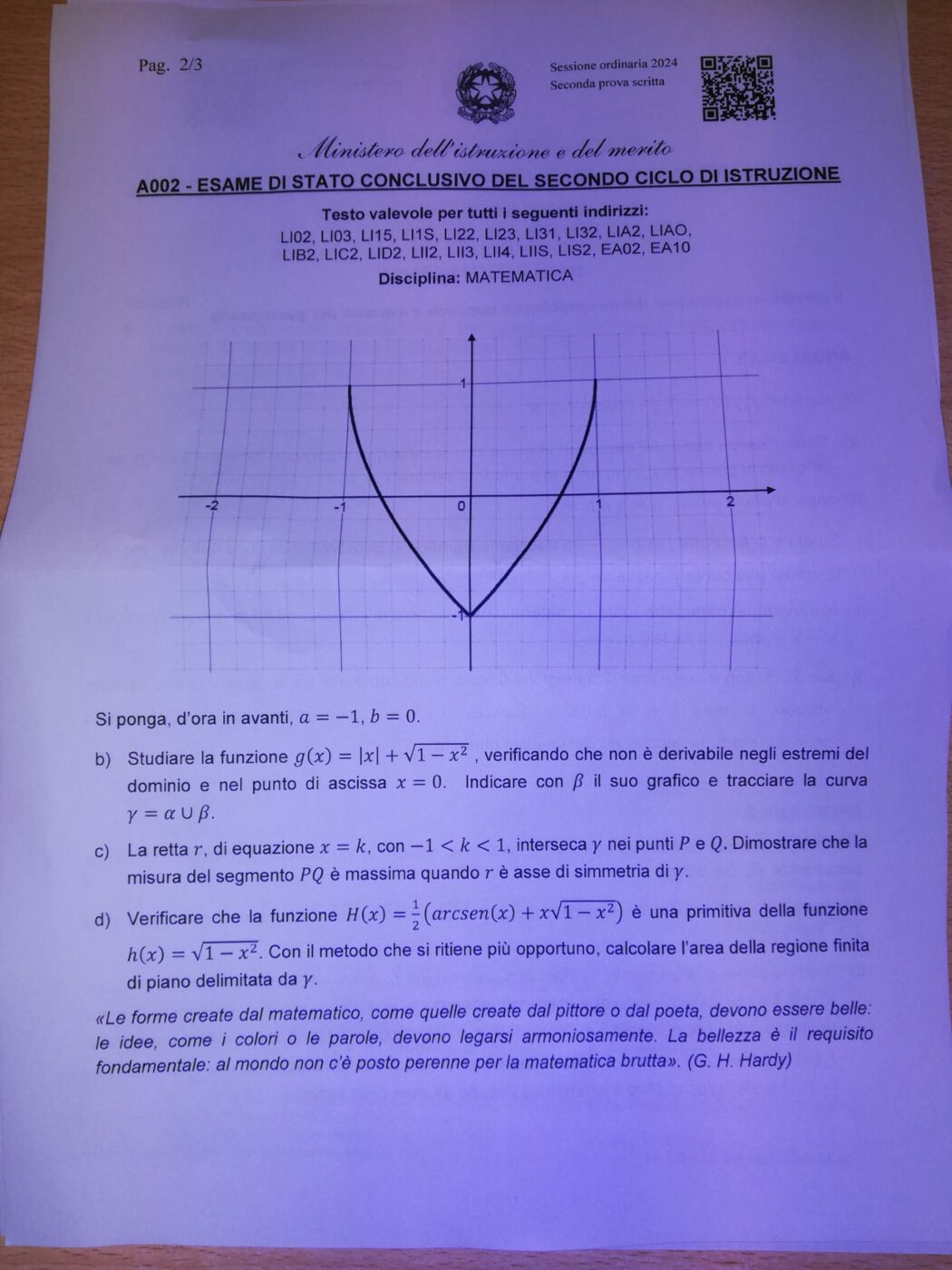
Il problema 2 è più difficile e gli studenti devono studiare un insieme di funzioni definite da un insieme di parametri. Per trovare la soluzione dell’ultimo punto bisogna poi conoscere la nozione di primitiva e saper calcolare l’area compresa tra delle curve.
Quesito 1
Si tratta di un problema dimostrativo di geometria euclidea: gli studenti devono fare attenzione alla presenza del “se e solo se”, che richiede di dividere la dimostrazione in due parti.
Quesito 2
Questo quesito fa riferimento al calcolo della distribuzione della probabilità in caso di prove ripetute e non dipendenti con soli due risultati possibili (distribuzione di Bernoulli). Il secondo punto rappresenta un problema di ottimizzazione, in quanto prevede l’applicazione della derivata prima rispetto a p della funzione e del calcolo dei punti di massimo (derivata uguale a 0).
Quesito 3
Il terzo è un problema di geometria nello spazio e gli studenti devono conoscere le nozioni di proiezione ortogonale di un punto su un piano data la sua equazione ed è necessario essere capaci di trovare una intersezione tra una retta e un piano entrambi scritti in forma cartesiana.
Quesito 4
Quarto quesito sulle caratteristiche delle funzioni continue, nozioni relative ai principali teoremi (teorema esistenza degli zeri), in cui è necessario dimostrare l’esistenza e unicità della soluzione.
Quesito 5
Nel quinto quesito gli studenti devono tradurre le condizioni sulla funzione e sulla sua derivata prima con lo scopo di creare un sistema di equazioni di primo grado per trovare l’espressione dell’equazione. Fondamentale la conoscenza della definizione di punto stazionario.
Quesito 6
Il quesito numero sei riguarda la risoluzione di un integrale definito tra una variabile il cui valore viene assegnato successivamente e un parametro ‘a’ del quale deve essere ricercato il massimo valore secondo la condizione F(2x)=-12. Per risolvere la funzione integrale bisogna usare l’integrale notevole: cos[f(x)]*f'(x) dx= sin[f(x)].
Quesito 7
Per risolvere il quesito numero sette è fondamentale avere delle conoscenze di geometria analitica, inoltre conoscere l’equazione dell’ellisse e soprattutto come ricavarla partendo dai semiassi (maggiore e minore che corrispondono ad afelio e perielio).
Quesito 8
L’ultimo quesito richiede di trovare il rapporto tra l’apotema di un esagono e il raggio della circonferenza circoscritta ad esso: in questo caso si possono utilizzare diversi approcci, per esempio un approccio di tipo trigonometrico.